Som van vierkanten formule snelkoppeling
 Share
Share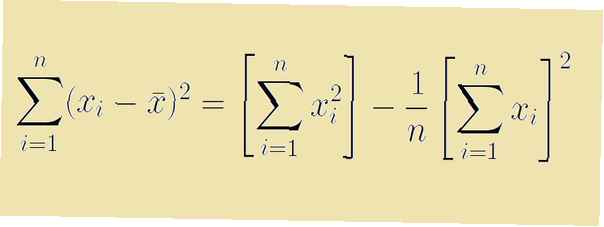
De berekening van een steekproefvariantie of standaarddeviatie wordt meestal als een breuk vermeld. De teller van deze breuk omvat een som van kwadratische afwijkingen van het gemiddelde. In statistieken is de formule voor deze totale som van vierkanten
Σ (xik - X)2
Hier verwijst het symbool x̄ naar het steekproefgemiddelde en het symbool Σ vertelt ons dat we de gekwadrateerde verschillen moeten optellen (xik - x̄) voor iedereen ik.
Hoewel deze formule werkt voor berekeningen, is er een equivalente, snelkoppelingsformule waarvoor we niet eerst het steekproefgemiddelde moeten berekenen. Deze sneltoetsformule voor de som van vierkanten is
Σ (xik2) - (Σ xik)2/n
Hier de variabele n verwijst naar het aantal gegevenspunten in onze steekproef.
Voorbeeld van standaardformule
Om te zien hoe deze sneltoetsformule werkt, zullen we een voorbeeld overwegen dat met beide formules wordt berekend. Stel dat onze steekproef 2, 4, 6, 8 is. Het steekproefgemiddelde is (2 + 4 + 6 + 8) / 4 = 20/4 = 5. Nu berekenen we het verschil van elk gegevenspunt met de gemiddelde 5.
- 2 - 5 = -3
- 4 - 5 = -1
- 6 - 5 = 1
- 8 - 5 = 3
We kwadrateren nu elk van deze nummers en voegen ze samen. (-3)2 + (-1)2 + 12 + 32 = 9 + 1 + 1 + 9 = 20.
Voorbeeld van sneltoetsformule
Nu gebruiken we dezelfde gegevensset: 2, 4, 6, 8, met de sneltoetsformule om de som van de vierkanten te bepalen. We kwadrateren eerst elk gegevenspunt en voegen ze samen: 22 + 42 + 62 + 82 = 4 + 16 + 36 + 64 = 120.
De volgende stap is het optellen van alle gegevens en het kwadraat van deze som: (2 + 4 + 6 + 8)2 = 400. We delen dit door het aantal gegevenspunten om 400/4 = 100 te verkrijgen.
We trekken dit aantal nu af van 120. Dit geeft ons dat de som van de gekwadrateerde afwijkingen 20 is. Dit was precies het getal dat we al hebben gevonden in de andere formule.
Hoe werkt dit?
Veel mensen accepteren de formule gewoon tegen de nominale waarde en hebben geen idee waarom deze formule werkt. Door een klein beetje algebra te gebruiken, kunnen we zien waarom deze sneltoetsformule equivalent is aan de standaard, traditionele manier om de som van de kwadratische afwijkingen te berekenen.
Hoewel er honderden, zo niet duizenden waarden in een gegevensset uit de echte wereld kunnen voorkomen, gaan we ervan uit dat er slechts drie gegevenswaarden zijn: x1 , X2, X3. Wat we hier zien, kan worden uitgebreid tot een gegevensset met duizenden punten.
We beginnen met op te merken dat (x1 + X2 + X3) = 3 x̄. De uitdrukking Σ (xik - X)2 = (x1 - X)2 + (X2 - X)2 + (X3 - X)2.
