De associatieve en commutatieve eigenschappen

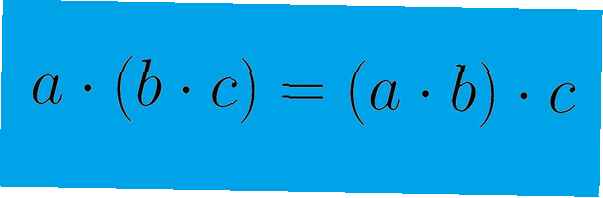
Er zijn verschillende wiskundige eigenschappen die worden gebruikt in statistieken en waarschijnlijkheid; twee hiervan, de commutatieve en associatieve eigenschappen, worden over het algemeen geassocieerd met de basisberekening van gehele getallen, rationele en reële getallen, hoewel ze ook worden weergegeven in meer geavanceerde wiskunde.

Deze eigenschappen - de commutatieve en de associatieve - lijken erg op elkaar en kunnen gemakkelijk worden verwisseld. Om die reden is het belangrijk om het verschil tussen de twee te begrijpen.

De commutatieve eigenschap betreft de volgorde van bepaalde wiskundige bewerkingen. Voor een binaire bewerking - een die slechts twee elementen omvat - kan dit worden weergegeven door de vergelijking a + b = b + a. De bewerking is commutatief omdat de volgorde van de elementen het resultaat van de bewerking niet beïnvloedt. De associatieve eigenschap heeft daarentegen betrekking op het groeperen van elementen in een operatie. Dit kan worden aangetoond door de vergelijking (a + b) + c = a + (b + c). De groepering van de elementen, zoals aangegeven tussen haakjes, heeft geen invloed op het resultaat van de vergelijking. Merk op dat wanneer de commutatieve eigenschap wordt gebruikt, elementen in een vergelijking zijn herschikte. Wanneer de associatieve eigenschap wordt gebruikt, zijn elementen slechts gehergroepeerd.

Gemeenschappelijk eigendom

Eenvoudig gezegd stelt de commutatieve eigenschap dat de factoren in een vergelijking vrij kunnen worden herschikt zonder de uitkomst van de vergelijking te beïnvloeden. De commutatieve eigenschap houdt zich daarom bezig met het ordenen van bewerkingen, inclusief het optellen en vermenigvuldigen van reële getallen, gehele getallen en rationale getallen.

De nummers 2, 3 en 5 kunnen bijvoorbeeld in elke volgorde worden opgeteld zonder het eindresultaat te beïnvloeden:

2 + 3 + 5 = 10

3 + 2 + 5 = 10

5 + 3 + 2 = 10

De getallen kunnen ook in elke volgorde worden vermenigvuldigd zonder het eindresultaat te beïnvloeden:

2 x 3 x 5 = 30

3 x 2 x 5 = 30

5 x 3 x 2 = 30

Aftrekken en delen zijn echter geen bewerkingen die commutatief kunnen zijn omdat de volgorde van bewerkingen belangrijk is. De drie bovenstaande nummers kan niet, bijvoorbeeld in willekeurige volgorde worden afgetrokken zonder de uiteindelijke waarde te beïnvloeden:

2 - 3 - 5 = -6

3 - 5 - 2 = -4

5 - 3 - 2 = 0