Wat zijn waarschijnlijkheid Axioma's?

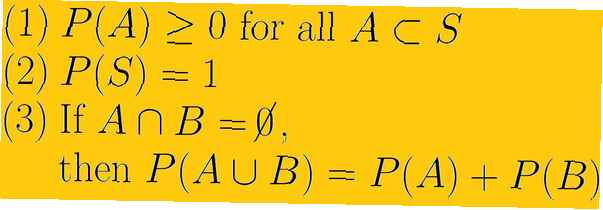
Een strategie in de wiskunde is om met enkele stellingen te beginnen en vervolgens meer wiskunde op te bouwen uit deze stellingen. De beginuitspraken staan ​​bekend als axioma's. Een axioma is typisch iets dat wiskundig vanzelfsprekend is. Uit een relatief korte lijst met axioma's wordt deductieve logica gebruikt om andere uitspraken te bewijzen, stellingen of stellingen genoemd.

Het gebied van wiskunde dat bekend staat als waarschijnlijkheid is niet anders. Waarschijnlijkheid kan worden teruggebracht tot drie axioma's. Dit werd voor het eerst gedaan door de wiskundige Andrei Kolmogorov. Het handjevol axioma's dat aan onderliggende waarschijnlijkheid ten grondslag ligt, kan worden gebruikt om allerlei resultaten af ​​te leiden. Maar wat zijn deze waarschijnlijkheid axioma's?

Definities en inleidingen

Om de axioma's voor waarschijnlijkheid te begrijpen, moeten we eerst enkele basisdefinities bespreken. We veronderstellen dat we een reeks resultaten hebben die de voorbeeldruimte wordt genoemd S. Deze voorbeeldruimte kan worden gezien als de universele set voor de situatie die we bestuderen. De voorbeeldruimte bestaat uit subsets die evenementen worden genoemd E₁, E₂,... , E_n. 

We gaan er ook van uit dat er een manier is om een ​​kans toe te kennen aan een gebeurtenis E. Dit kan worden gezien als een functie met een set voor een invoer en een reëel getal als uitvoer. De waarschijnlijkheid van het evenement E wordt aangegeven door P(E).

Axioma One

Het eerste axioma van waarschijnlijkheid is dat de waarschijnlijkheid van een gebeurtenis een niet-negatief reëel getal is. Dit betekent dat de kleinste kans die ooit kan zijn nul is en dat deze niet oneindig kan zijn. De reeks getallen die we kunnen gebruiken, zijn reële getallen. Dit verwijst naar zowel rationale getallen, ook wel breuken genoemd, en irrationele getallen die niet als breuken kunnen worden geschreven.

Een ding om op te merken is dat dit axioma niets zegt over hoe groot de kans op een gebeurtenis kan zijn. Het axioma elimineert de mogelijkheid van negatieve waarschijnlijkheden. Het weerspiegelt het idee dat de kleinste waarschijnlijkheid, gereserveerd voor onmogelijke gebeurtenissen, nul is.

Axioma twee

Het tweede axioma van waarschijnlijkheid is dat de waarschijnlijkheid van de gehele monsterruimte één is. Symbolisch schrijven we P(S) = 1. Impliciet in dit axioma is het idee dat de steekproefruimte alles mogelijk is voor ons waarschijnlijkheidsexperiment en dat er geen gebeurtenissen buiten de steekproefruimte zijn.

Op zichzelf stelt dit axioma geen bovengrens voor de waarschijnlijkheden van gebeurtenissen die niet de gehele steekproefruimte zijn. Het geeft wel weer dat iets met absolute zekerheid een kans van 100% heeft.

Axioma Drie

Het derde axioma van waarschijnlijkheid gaat over elkaar uitsluitende gebeurtenissen. Als E₁ en E₂ sluiten elkaar uit, wat betekent dat ze een lege kruising hebben en we gebruiken U om de unie aan te duiden P(E₁ U E₂ ) = P(E₁) + P(E₂).

Het axioma bestrijkt de situatie eigenlijk met verschillende (zelfs ontelbaar oneindige) gebeurtenissen, die elk wederzijds exclusief zijn. Zolang dit gebeurt, is de waarschijnlijkheid van de vereniging van de gebeurtenissen hetzelfde als de som van de waarschijnlijkheden:

P(E₁ U E₂ U ... U E_n ) = P(E₁) + P(E₂) + ... + E_n

Hoewel dit derde axioma misschien niet zo nuttig lijkt, zullen we zien dat het in combinatie met de andere twee axioma's inderdaad behoorlijk krachtig is.

Axiom-toepassingen

De drie axioma's stellen een bovengrens voor de waarschijnlijkheid van een gebeurtenis. We duiden het complement van het evenement aan E door E^C. Van verzamelingenleer, E en E^C hebben een lege kruising en sluiten elkaar uit. voorts E U E^C = S, de hele monsterruimte.

Deze feiten, gecombineerd met de axioma's, geven ons: