The Number Pi 3.14159265…

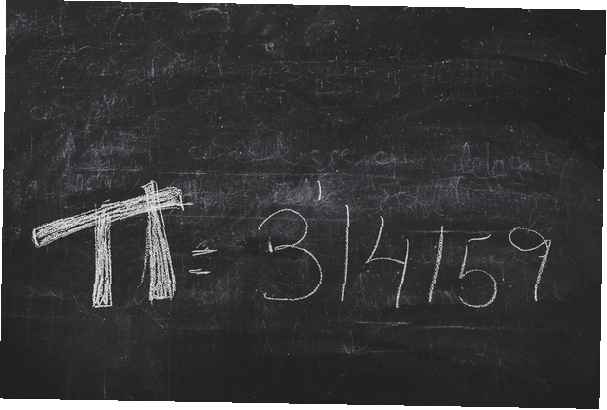
Een van de meest gebruikte constanten in de wiskunde is het getal pi, dat wordt aangeduid met de Griekse letter π. Het concept van pi is ontstaan ​​in de geometrie, maar dit aantal heeft toepassingen in de hele wiskunde en komt voor in uiteenlopende onderwerpen, waaronder statistieken en waarschijnlijkheid. Pi heeft zelfs culturele erkenning en een eigen vakantie gekregen, met de viering van Pi Day-activiteiten over de hele wereld.

De waarde van Pi

Pi wordt gedefinieerd als de verhouding tussen de omtrek van een cirkel en zijn diameter. De waarde van pi is iets groter dan drie, wat betekent dat elke cirkel in het universum een ​​omtrek heeft met een lengte die iets meer dan drie keer zijn diameter is. Meer precies, pi heeft een decimale weergave die begint met 3.14159265 ... Dit is slechts een deel van de decimale uitbreiding van pi.

Pi-feiten

Pi heeft veel fascinerende en ongewone functies, waaronder: 

• Pi is een irrationeel reëel getal. Dit betekent dat pi niet als een breuk kan worden uitgedrukt a / b waar een en b zijn beide gehele getallen. Hoewel de getallen 22/7 en 355/113 nuttig zijn bij het schatten van pi, is geen van deze fracties de werkelijke waarde van pi.
• Omdat pi een irrationeel getal is, wordt de decimale uitbreiding ervan nooit beëindigd of herhaald. Er zijn enkele vragen met betrekking tot deze decimale uitbreiding, zoals: Verschijnt elke mogelijke reeks cijfers ergens in de decimale uitbreiding van pi? Als elke mogelijke string verschijnt, dan is je mobiele nummer ergens in de uitbreiding van pi (maar dat geldt ook voor iedereen).
• Pi is een transcendentaal getal. Dit betekent dat pi niet de nul is van een polynoom met gehele coëfficiënten. Dit feit is belangrijk bij het verkennen van meer geavanceerde functies van pi.
• Pi is geometrisch belangrijk, en niet alleen omdat het de omtrek en diameter van een cirkel relateert. Dit nummer wordt ook weergegeven in de formule voor het gebied van een cirkel. Het gebied van een straalcirkel r is EEN = pi r². Het getal pi wordt gebruikt in andere geometrische formules, zoals het oppervlak en het volume van een bol, het volume van een kegel en het volume van een cilinder met een cirkelvormige basis.
• Pi verschijnt wanneer het minst verwacht. Overweeg voor een van de vele voorbeelden hiervan de oneindige som 1 + 1/4 + 1/9 + 1/16 + 1/25 + ... Deze som komt overeen met de waarde pi²/ 6.

Pi in statistiek en waarschijnlijkheid

Pi maakt verrassende verschijningen in de hele wiskunde, en sommige van deze verschijningen hebben betrekking op waarschijnlijkheid en statistiek. De formule voor de standaard normale verdeling, ook bekend als de belcurve, heeft het getal pi als een normalisatieconstante. Met andere woorden, door te delen door een uitdrukking waarbij pi is betrokken, kunt u zeggen dat het gebied onder de curve gelijk is aan één. Pi maakt ook deel uit van de formules voor andere kansverdelingen.

Een ander verrassend voorval van pi is waarschijnlijk een eeuwenoud experiment met naald gooien. In de 18e eeuw, Georges-Louis Leclerc, stelde Comte de Buffon een vraag over de waarschijnlijkheid van het laten vallen van naalden: begin met een vloer met planken van een uniforme breedte waarin de lijnen tussen elk van de planken evenwijdig aan elkaar zijn. Neem een ​​naald met een lengte korter dan de afstand tussen de planken. Als u een naald op de vloer laat vallen, hoe groot is de kans dat deze op een lijn tussen twee van de houten planken zal landen?

Het blijkt dat de kans dat de naald op een lijn tussen twee planken landt twee keer de lengte van de naald gedeeld door de lengte tussen de planken maal pi.