Theorie instellen

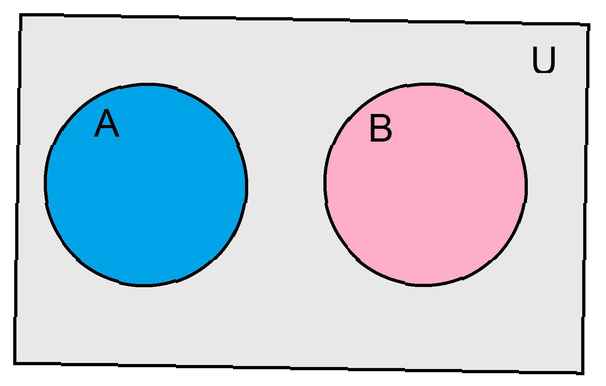
De verzamelingenleer is een fundamenteel concept in de gehele wiskunde. Deze tak van wiskunde vormt een basis voor andere onderwerpen. 

Intuïtief is een set een verzameling objecten, die elementen worden genoemd. Hoewel dit een eenvoudig idee lijkt, heeft het enkele verstrekkende gevolgen. 

Elements

De elementen van een set kunnen echt alles zijn - getallen, staten, auto's, mensen of zelfs andere sets zijn allemaal mogelijkheden voor elementen. Zowat alles dat samen kan worden verzameld, kan worden gebruikt om een ​​set te vormen, hoewel er enkele dingen zijn waar we voorzichtig mee moeten zijn.

Gelijke sets

Elementen van een set zitten in een set of niet in een set. We kunnen een set beschrijven aan de hand van een definiërende eigenschap, of we kunnen de elementen in de set vermelden. De volgorde waarin ze worden vermeld, is niet belangrijk. Dus de sets 1, 2, 3 en 1, 3, 2 zijn gelijke sets, omdat ze beide dezelfde elementen bevatten.

Twee speciale sets

Twee sets verdienen speciale vermelding. De eerste is de universele set, meestal aangeduid U. Deze set bevat alle elementen waaruit we kunnen kiezen. Deze set kan verschillen van instelling tot instelling. Eén universele set kan bijvoorbeeld de set reële getallen zijn, terwijl voor een ander probleem de universele set de hele getallen 0, 1, 2, ... kan zijn. 

De andere set die enige aandacht vereist, wordt de lege set genoemd. De lege set is de unieke set is de set zonder elementen. We kunnen dit schrijven als en deze set aangeven met het symbool ∅.

Subsets en de Power Set

Een verzameling van enkele elementen van een set EEN wordt een subset van genoemd EEN. Wij zeggen dat EEN is een subset van B als en alleen als elk element van EEN is ook een element van B. Als er een eindig nummer is n elementen in een set, dan zijn er in totaal 2ⁿ subsets van EEN. Deze verzameling van alle subsets van EEN is een set die de power set van wordt genoemd EEN.

Bewerkingen instellen

Net zoals we bewerkingen zoals optellen kunnen uitvoeren - op twee nummers om een ​​nieuw nummer te verkrijgen, worden set-theorie-bewerkingen gebruikt om een ​​set uit twee andere sets te vormen. Er zijn een aantal bewerkingen, maar bijna alle zijn samengesteld uit de volgende drie bewerkingen:

• Unie - Een unie betekent een samenbrengen. De vereniging van de sets EEN en B bestaat uit de elementen die zich in een van beide bevinden EEN of B.
• Kruising - Een kruising is waar twee dingen elkaar ontmoeten. Het snijpunt van de sets EEN en B bestaat uit de elementen die in beide EEN en B.
• Complement - Het complement van de set EEN bestaat uit alle elementen in de universele set die geen elementen van zijn EEN.

Venn diagrammen

Een hulpmiddel dat nuttig is bij het weergeven van de relatie tussen verschillende sets wordt een Venn-diagram genoemd. Een rechthoek vertegenwoordigt de universele set voor ons probleem. Elke set wordt weergegeven met een cirkel. Als de cirkels elkaar overlappen, illustreert dit de kruising van onze twee sets. 

Toepassingen van Set Theory

Set-theorie wordt overal in de wiskunde gebruikt. Het wordt gebruikt als basis voor vele subvelden van de wiskunde. In de gebieden die betrekking hebben op statistieken, wordt het vooral in de waarschijnlijkheid gebruikt. Veel van de waarschijnlijkheidsconcepten zijn afgeleid van de consequenties van de verzamelingenleer. Inderdaad, een manier om de axioma's van waarschijnlijkheid te stellen, is de settheorie.