Werkblad over combinaties en permutaties

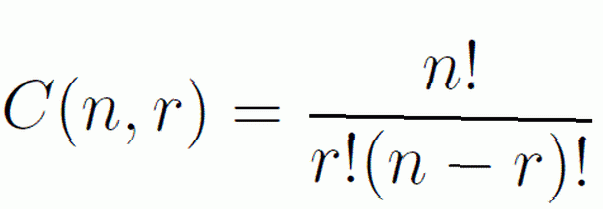
Permutaties en combinaties zijn twee concepten die verband houden met waarschijnlijkheidsideeën. Deze twee onderwerpen lijken erg op elkaar en zijn gemakkelijk in de war te raken. In beide gevallen beginnen we met een set met een totaal van n elementen. Dan tellen we r van deze elementen. De manier waarop we deze elementen tellen, bepaalt of we met een combinatie of met een permutatie werken.

Bestellen en rangschikken

De belangrijkste dingen om te onthouden bij het onderscheid tussen combinaties en permutaties hebben te maken met orde en arrangementen. Permutaties gaan over situaties waarin de volgorde waarin we de objecten kiezen belangrijk is. We kunnen dit ook beschouwen als gelijkwaardig aan het idee om objecten te rangschikken

In combinaties maken we ons niet bezig met de volgorde waarin we onze objecten hebben geselecteerd. We hebben alleen dit concept nodig, en de formules voor combinaties en permutaties om problemen met dit onderwerp op te lossen.

Oefen problemen

Om ergens goed in te worden, is enige oefening nodig. Hier zijn enkele oefenproblemen met oplossingen om u te helpen de ideeën van permutaties en combinaties recht te trekken. Een versie met antwoorden is hier. Nadat u bent begonnen met alleen basisberekeningen, kunt u met wat u weet bepalen of naar een combinatie of permutatie wordt verwezen.

1. Gebruik de formule voor permutaties om te berekenen P(5, 2).
2. Gebruik de formule voor combinaties om te berekenen C(5, 2).
3. Gebruik de formule voor permutaties om te berekenen P(6, 6).
4. Gebruik de formule voor combinaties om te berekenen C(6, 6).
5. Gebruik de formule voor permutaties om te berekenen P(100, 97).
6. Gebruik de formule voor combinaties om te berekenen C(100, 97).
7. Het is de verkiezingstijd op een middelbare school met in totaal 50 studenten in de junior class. Hoeveel manieren kunnen een klassenpresident, klassen vice president, klassenpenningmeester en klassensecretaris worden gekozen als elke student slechts één kantoor mag hebben?
8. Dezelfde klas van 50 studenten wil een prom-commissie vormen. Hoeveel manieren kan een vierpersoons prom-commissie worden gekozen uit de junior class?
9. Als we een groep van vijf studenten willen vormen en we hebben 20 om uit te kiezen, hoeveel manieren is dit mogelijk?
10. Hoeveel manieren kunnen we vier letters van het woord "computer" rangschikken als herhalingen niet zijn toegestaan, en verschillende volgorde van dezelfde letters tellen als verschillende arrangementen?
11. Hoeveel manieren kunnen we vier letters van het woord "computer" rangschikken als herhalingen niet zijn toegestaan, en verschillende volgorde van dezelfde letters tellen als hetzelfde arrangement?
12. Hoeveel verschillende viercijferige nummers zijn mogelijk als we cijfers van 0 tot 9 kunnen kiezen en alle cijfers moeten verschillend zijn?
13. Als we een doos met zeven boeken krijgen, op hoeveel manieren kunnen we er drie op een plank plaatsen?
14. Als we een doos met zeven boeken krijgen, hoeveel manieren kunnen we dan een verzameling van drie boeken uit de doos kiezen?