Wat zijn residuen?

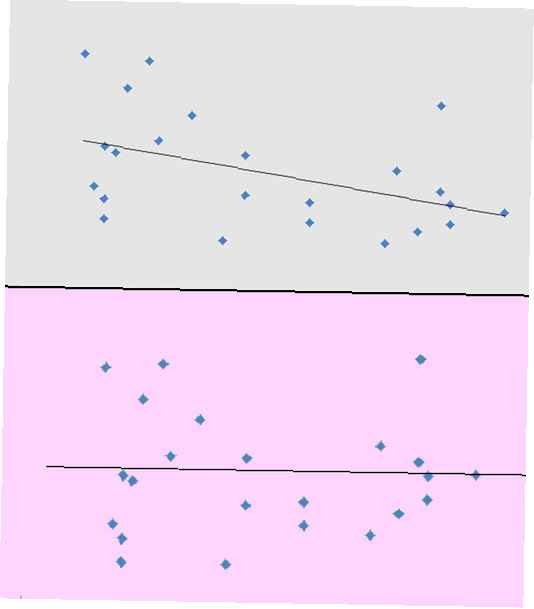
Lineaire regressie is een statistisch hulpmiddel dat bepaalt hoe goed een rechte lijn past bij een set gepaarde gegevens. De rechte lijn die het beste bij die gegevens past, wordt de regressielijn van de kleinste kwadraten genoemd. Deze lijn kan op verschillende manieren worden gebruikt. Een van deze toepassingen is het schatten van de waarde van een responsvariabele voor een gegeven waarde van een verklarende variabele. Gerelateerd aan dit idee is dat van een reststof.

Residuen worden verkregen door aftrekken. Het enige dat we moeten doen, is de voorspelde waarde van aftrekken Y van de waargenomen waarde van Y voor een bepaalde X. Het resultaat wordt een restwaarde genoemd.

Formule voor residuen

De formule voor residuen is eenvoudig:

Rest = waargenomen Y - voorspelde Y

Het is belangrijk op te merken dat de voorspelde waarde afkomstig is van onze regressielijn. De waargenomen waarde komt uit onze gegevensset.

Voorbeelden

We zullen het gebruik van deze formule illustreren aan de hand van een voorbeeld. Stel dat we de volgende set gepaarde gegevens krijgen:

(1, 2), (2, 3), (3, 7), (3, 6), (4, 9), (5, 9)

Door software te gebruiken kunnen we zien dat de regressielijn van de kleinste kwadraten is Y = 2X. We zullen dit gebruiken om waarden te voorspellen voor elke waarde van X.

Bijvoorbeeld wanneer X = 5 zien we dat 2 (5) = 10. Dit geeft ons het punt langs onze regressielijn met een X coördinaat van 5.

Om het residu op de punten te berekenen X = 5, we trekken de voorspelde waarde af van onze waargenomen waarde. Sinds de Y coördinaat van ons gegevenspunt was 9, dit geeft een restwaarde van 9 - 10 = -1.

In de volgende tabel zien we hoe we al onze residuen voor deze gegevensset kunnen berekenen:

X	Waargenomen y	Voorspeld y	overgebleven
1	2	2	0
2	3	4	-1
3	7	6	1
3	6	6	0
4	9	8	1
5	9	10	-1

Kenmerken van residuen

Nu we een voorbeeld hebben gezien, zijn er een paar kenmerken van resten om op te merken:

• Residuen zijn positief voor punten die boven de regressielijn vallen.
• Residuen zijn negatief voor punten die onder de regressielijn vallen.
• Residuen zijn nul voor punten die precies langs de regressielijn vallen.
• Hoe groter de absolute waarde van het residu, hoe verder het punt van de regressielijn ligt.
• De som van alle residuen moet nul zijn. In de praktijk is deze som soms niet precies nul. De reden voor dit verschil is dat afrondingsfouten zich kunnen ophopen.

Gebruik van residuen

Er zijn verschillende toepassingen voor residuen. Eén gebruik is om ons te helpen te bepalen of we een gegevensset hebben met een algemene lineaire trend, of dat we een ander model moeten overwegen. De reden hiervoor is dat residuen helpen bij het versterken van elk niet-lineair patroon in onze gegevens. Wat moeilijk te zien is door naar een spreidingsdiagram te kijken, kan gemakkelijker worden waargenomen door de residuen te onderzoeken en een bijbehorend restdiagram.

Een andere reden om residuen te overwegen is om te controleren of aan de voorwaarden voor inferentie voor lineaire regressie is voldaan. Na verificatie van een lineaire trend (door de residuen te controleren), controleren we ook de verdeling van de residuen. Om regressie-inferentie te kunnen uitvoeren, willen we dat de residuen rond onze regressielijn ongeveer normaal verdeeld zijn. Een histogram of stamplot van de residuen helpt om te verifiëren dat aan deze voorwaarde is voldaan.