Inleiding tot de Dirac Delta-functie
 Share
Share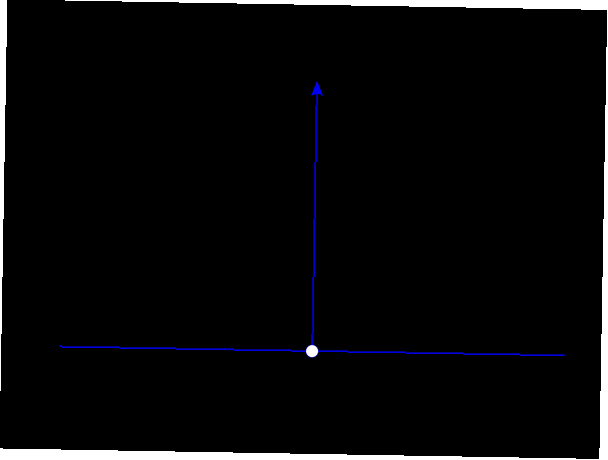
De Dirac-deltafunctie is de naam die wordt gegeven aan een wiskundige structuur die bedoeld is om een geïdealiseerd puntobject weer te geven, zoals een puntmassa of puntlading. Het heeft brede toepassingen binnen de kwantummechanica en de rest van de kwantumfysica, omdat het meestal wordt gebruikt in de kwantumgolffunctie. De delta-functie wordt weergegeven met het Griekse symbool delta in kleine letters, geschreven als een functie: δ (X).
Hoe de deltafunctie werkt
Deze weergave wordt bereikt door de Dirac-deltafunctie zo te definiëren dat deze overal een waarde van 0 heeft, behalve bij de invoerwaarde van 0. Op dat moment vertegenwoordigt het een piek die oneindig hoog is. De integraal over de hele lijn is gelijk aan 1. Als je calculus hebt bestudeerd, kom je dit fenomeen waarschijnlijk al eerder tegen. Houd er rekening mee dat dit een concept is dat normaal gesproken aan studenten wordt geïntroduceerd na jaren van college-niveau studie in theoretische fysica.
Met andere woorden, de resultaten zijn de volgende voor de meest elementaire deltafunctie δ (X), met een eendimensionale variabele X, voor enkele willekeurige invoerwaarden:
- 8 (5) = 0
- 8 (-20) = 0
- 8 (38,4) = 0
- 8 (-12,2) = 0
- 8 (0,11) = 0
- δ (0) = ∞
U kunt de functie opschalen door deze met een constante te vermenigvuldigen. Volgens de rekenregels zal vermenigvuldiging met een constante waarde ook de waarde van de integraal met die constante factor verhogen. Sinds de integraal van δ (X) over alle reële getallen 1 is, dan zou het vermenigvuldigen met een constante van een nieuwe integraal hebben die gelijk is aan die constante. Dus bijvoorbeeld 27δ (X) heeft een integraal voor alle reële getallen van 27.
Een ander handig ding om te overwegen is dat, omdat de functie een niet-nulwaarde heeft alleen voor een invoer van 0, en als u naar een coördinatenraster kijkt waar uw punt niet precies op 0 staat, dit kan worden weergegeven met een uitdrukking in de functie-invoer. Dus als je het idee wilt weergeven dat het deeltje zich op een positie bevindt X = 5, dan zou je de Dirac delta-functie schrijven als δ (x - 5) = ∞ [sinds δ (5 - 5) = ∞].
Als u deze functie vervolgens wilt gebruiken om een reeks puntdeeltjes binnen een kwantumsysteem weer te geven, kunt u dit doen door verschillende dirac delta-functies bij elkaar op te tellen. Voor een concreet voorbeeld kan een functie met punten op x = 5 en x = 8 worden weergegeven als δ (x - 5) + δ (x - 8). Als u vervolgens een integraal van deze functie over alle getallen zou nemen, zou u een integraal krijgen die reële getallen vertegenwoordigt, hoewel de functies 0 zijn op alle locaties behalve de twee waar er punten zijn. Dit concept kan vervolgens worden uitgebreid om een ruimte met twee of drie dimensies weer te geven (in plaats van het eendimensionale geval dat ik in mijn voorbeelden heb gebruikt).
Dit is weliswaar een korte inleiding tot een zeer complex onderwerp. Het belangrijkste dat u zich hiervan moet realiseren, is dat de Dirac-deltafunctie in feite bestaat met als enig doel de integratie van de functie zinvol te maken. Wanneer er geen integraal plaatsvindt, is de aanwezigheid van de Dirac delta-functie niet bijzonder nuttig. Maar in de natuurkunde, als je te maken hebt met het gaan van een regio zonder deeltjes die plotseling op slechts één punt bestaan, is het heel nuttig.
Bron van de deltafunctie
In zijn boek uit 1930, Principes van kwantummechanica, De Engelse theoretisch fysicus Paul Dirac legde de belangrijkste elementen van de kwantummechanica uit, inclusief de notatie van de rem en ook zijn Dirac-deltafunctie. Dit werden standaardconcepten op het gebied van de kwantummechanica binnen de Schrodinger-vergelijking.
