Z-Scores werkblad

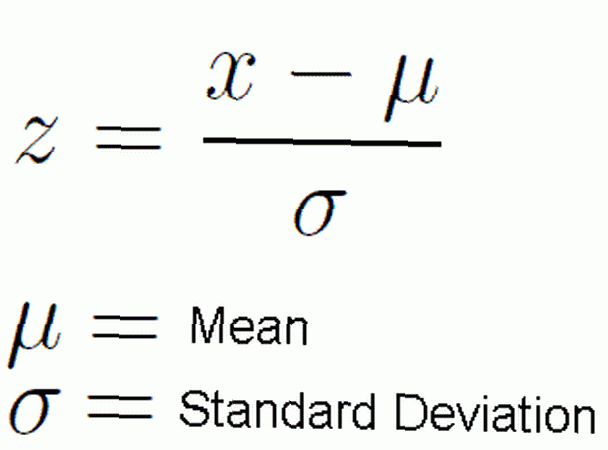
Een standaardtype probleem van een inleidende statistiekcursus is het berekenen van de z-score van een bepaalde waarde. Dit is een zeer eenvoudige berekening, maar is er een die heel belangrijk is. De reden hiervoor is dat we hiermee door het oneindige aantal normale distributies kunnen waden. Deze normale verdelingen kunnen elke gemiddelde of positieve standaardafwijking hebben.

De z-scoreformule begint met dit oneindige aantal verdelingen en laat ons alleen werken met de standaard normale verdeling. In plaats van te werken met een andere normale distributie voor elke toepassing die we tegenkomen, hoeven we alleen met één speciale normale distributie te werken. De standaard normale verdeling is deze goed bestudeerde verdeling.  

Uitleg van het proces

We gaan ervan uit dat we werken in een omgeving waarin onze gegevens normaal worden verspreid. We nemen ook aan dat ons het gemiddelde en de standaarddeviatie wordt gegeven van de normale verdeling waarmee we werken. Door de z-score formule te gebruiken: z = (X - μ) / σ we kunnen elke verdeling omzetten in de standaard normale verdeling. Hier is de Griekse letter μ het gemiddelde en σ de standaardafwijking. 

De standaard normale verdeling is een speciale normale verdeling. Het heeft een gemiddelde van 0 en de standaardafwijking is gelijk aan 1.

Z-score problemen

Alle volgende problemen maken gebruik van de z-score formule. Al deze oefenproblemen betreffen het vinden van een z-score uit de verstrekte informatie. Kijk of je erachter kunt komen hoe je deze formule kunt gebruiken.

1. Scores op een geschiedenistest hebben gemiddeld 80 met standaarddeviatie van 6. Wat is het z-score voor een student die een 75 op de test heeft verdiend?
2. Het gewicht van chocoladerepen van een bepaalde chocoladefabriek heeft een gemiddelde van 8 gram met een standaarddeviatie van 0,1 gram. Wat is de z-score die overeenkomt met een gewicht van 8,17 ounces?
3. Boeken in de bibliotheek hebben een gemiddelde lengte van 350 pagina's met een standaarddeviatie van 100 pagina's. Wat is de z-score die overeenkomt met een boek met een lengte van 80 pagina's?
4. De temperatuur wordt geregistreerd op 60 luchthavens in een regio. De gemiddelde temperatuur is 67 graden Fahrenheit met standaardafwijking van 5 graden. Wat is de z-score voor een temperatuur van 68 graden?
5. Een groep vrienden vergelijkt wat ze hebben ontvangen tijdens trick or treat. Ze vinden dat het gemiddelde aantal ontvangen snoepjes 43 is, met een standaarddeviatie van 2. Wat is het z-score die overeenkomt met 20 snoepjes?
6. De gemiddelde groei van de dikte van bomen in een bos blijkt 0,5 cm / jaar te zijn met een standaardafwijking van 0,1 cm / jaar. Wat is de z-score die overeenkomt met 1 cm / jaar?
7. Een bepaald been voor dinosaurusfossielen heeft een gemiddelde lengte van 5 voet met standaardafwijking van 3 duim. Wat is de z-score die overeenkomt met een lengte van 62 inch?

Nadat u deze problemen hebt opgelost, moet u uw werk controleren. Of misschien als je vastzit in wat je moet doen. Oplossingen met enkele verklaringen vindt u hier.