De complementregel

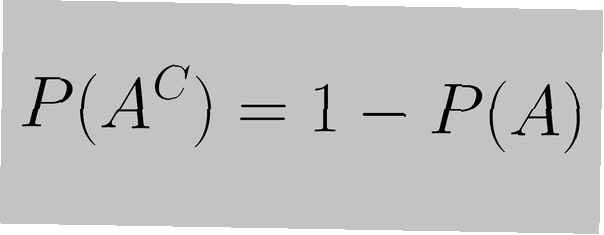
In de statistiek is de complementregel een stelling die een verband biedt tussen de waarschijnlijkheid van een gebeurtenis en de waarschijnlijkheid van de aanvulling van de gebeurtenis op een zodanige manier dat als we een van deze waarschijnlijkheden kennen, we automatisch de andere kennen.

De complementregel is handig wanneer we bepaalde kansen berekenen. Vaak is de waarschijnlijkheid van een gebeurtenis rommelig of ingewikkeld om te berekenen, terwijl de waarschijnlijkheid van het complement ervan veel eenvoudiger is.

Voordat we zien hoe de complementregel wordt gebruikt, zullen we specifiek definiëren wat deze regel is. We beginnen met een beetje notatie. Het complement van het evenement EEN, bestaande uit alle elementen in de voorbeeldruimte S dat zijn geen elementen van de set EEN, wordt aangegeven door EENC.

Verklaring van de complementregel

De complementregel wordt vermeld als "de som van de waarschijnlijkheid van een gebeurtenis en de waarschijnlijkheid van zijn complement is gelijk aan 1", zoals uitgedrukt door de volgende vergelijking:

P (EEN^C) = 1 - P (EEN)

Het volgende voorbeeld laat zien hoe de complementregel moet worden gebruikt. Het zal duidelijk worden dat deze stelling de kansberekeningen zowel versnelt als vereenvoudigt.

Waarschijnlijkheid zonder de complementregel

Stel dat we acht eerlijke munten omdraaien - wat is de kans dat we minstens één hoofd laten zien? Een manier om dit uit te zoeken is om de volgende kansen te berekenen. De noemer van elk wordt verklaard door het feit dat er 2 zijn⁸ = 256 resultaten, elk even waarschijnlijk. Al het volgende geeft ons een formule voor combinaties:

• De kans om precies één kop om te draaien is C (8,1) / 256 = 8/256.
• De kans om precies twee koppen om te draaien is C (8,2) / 256 = 28/256.
• De kans om precies drie koppen om te draaien is C (8,3) / 256 = 56/256.
• De kans om precies vier koppen om te draaien is C (8,4) / 256 = 70/256.
• De kans om precies vijf koppen om te draaien is C (8,5) / 256 = 56/256.
• De kans om precies zes koppen om te draaien is C (8,6) / 256 = 28/256.
• De kans om precies zeven koppen om te draaien is C (8,7) / 256 = 8/256.
• De kans om precies acht koppen om te draaien is C (8,8) / 256 = 1/256.

Dit zijn elkaar uitsluitende gebeurtenissen, dus we sommen de kansen samen op met behulp van de juiste toevoegingsregel. Dit betekent dat de kans dat we ten minste één hoofd hebben 255 van de 256 is.

De complementregel gebruiken om waarschijnlijkheidsproblemen te vereenvoudigen

We berekenen nu dezelfde kans met behulp van de complementregel. Het complement van de gebeurtenis "We draaien ten minste één kop" is de gebeurtenis "Er zijn geen koppen." Er is een manier om dit te laten gebeuren, waardoor we de kans hebben op 1/256. We gebruiken de complementregel en vinden dat onze gewenste kans één minus één op 256 is, wat gelijk is aan 255 van 256.

Dit voorbeeld toont niet alleen het nut, maar ook de kracht van de complementregel. Hoewel er niets mis is met onze oorspronkelijke berekening, was het behoorlijk ingewikkeld en vereiste het meerdere stappen. Toen we daarentegen de complementregel voor dit probleem gebruikten, waren er niet zoveel stappen waar de berekeningen mis konden gaan.