Standaard normale verdeling in wiskundige problemen

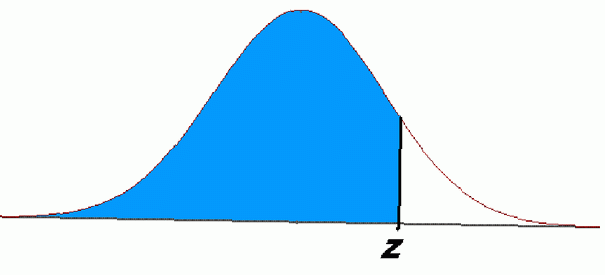
De standaard normale verdeling, beter bekend als de belcurve, verschijnt op verschillende plaatsen. Gewoonlijk worden verschillende gegevensbronnen gedistribueerd. Als gevolg van dit feit kan onze kennis over de standaard normale distributie worden gebruikt in een aantal toepassingen. Maar we hoeven niet voor elke toepassing met een andere normale verdeling te werken. In plaats daarvan werken we met een normale verdeling met een gemiddelde van 0 en een standaarddeviatie van 1. We zullen enkele toepassingen van deze verdeling bekijken die allemaal aan een bepaald probleem zijn gekoppeld.

Voorbeeld

Stel dat ons wordt verteld dat de hoogten van volwassen mannen in een bepaalde regio van de wereld normaal verdeeld zijn met een gemiddelde van 70 inch en een standaardafwijking van 2 inch.

1. Ongeveer welk deel van de volwassen mannen is groter dan 73 inch?
2. Welk aandeel volwassen mannen is tussen de 72 en 73 centimeter?
3. Welke lengte komt overeen met het punt waar 20% van alle volwassen mannen groter is dan deze lengte?
4. Welke lengte komt overeen met het punt waar 20% van alle volwassen mannen minder is dan deze lengte?

Oplossingen

Voordat je verdergaat, moet je stoppen en je werk doornemen. Een gedetailleerde uitleg van elk van deze problemen volgt hieronder:

1. Wij gebruiken onze z-scoreformule om 73 om te zetten naar een gestandaardiseerde score. Hier berekenen we (73 - 70) / 2 = 1,5. Dus de vraag wordt: wat is het gebied onder de standaard normale verdeling voor z groter dan 1,5? Raadpleeg onze tabel van z-scores tonen aan dat 0,933 = 93,3% van de gegevensverdeling minder is dan z = 1,5. Daarom zijn 100% - 93,3% = 6,7% van de volwassen mannen langer dan 73 inch.
2. Hier zetten we onze hoogten om naar een gestandaardiseerde z-scoren. We hebben gezien dat 73 dat heeft gedaan een z score van 1,5. De z-score van 72 is (72 - 70) / 2 = 1. We zijn dus op zoek naar het gebied onder de normale verdeling voor 1<z < 1.5. A quick check of the normal distribution table shows that this proportion is 0.933 - 0.841 = 0.092 = 9.2%
3. Hier is de vraag omgekeerd van wat we al hebben overwogen. Nu kijken we omhoog in onze tabel om een ​​te vinden z-partituur Z^* dat komt overeen met een oppervlakte van 0,200 hierboven. Voor gebruik in onze tabel merken we op dat dit is waar 0,800 lager is. Als we naar de tafel kijken, zien we dat z^* = 0,84. We moeten dit nu converteren z-scoren tot een hoogte. Aangezien 0,84 = (x - 70) / 2, betekent dit dat X = 71,68 inch.
4. We kunnen de symmetrie van de normale verdeling gebruiken en onszelf de moeite besparen om de waarde op te zoeken z^*. In plaats van z^* = 0,84, we hebben -0,84 = (x - 70) / 2. Dus X = 68,32 inch.

Het gebied van het gearceerde gebied links van z in het bovenstaande diagram toont deze problemen. Deze vergelijkingen vertegenwoordigen waarschijnlijkheden en hebben talloze toepassingen in statistieken en waarschijnlijkheid.